• System hierarchy: It allows defining system components in a hierarchical way, allowing to specify parameter (boundry) diagram and FMECA table of each sub-system independently.
• Parameter Diagram: It enables drawing parameter diagram of each sub-system of a system in a graphical editor.
• FMECA table: It enables specifying FMECA table of each sub-system.
• Automatic generation of fault trees: It enables automatic generation of fault trees from FMECA tables.
• Automatic generation of master logic diagrams: It enables automatic generation of master logic diagram from FMECA tables.

• Static & dynamic fault trees: It supports all static and dynamic fault tree gates for modeling fault-tolerant dynamic systems having redundancy, probabilistic functional dependencies, and temporal failure-ordering.
• Spare races: It can model and analyze situations where two or more subsystems try to get a shared spare component simultaneously, which might generate different analysis results, e.g., reliability.
• Automatic fault trees generation: It supports automatic generation of fault trees from FMEA data.
• Boolean logic definable events: It allows the definition of failure events through Boolean logic equations over fault tree gates.
• Model-based safety analysis: It allows for automatically extracting DFTs out of SysML v2 models annotated with safety information.
• Interactive simulation: It provides a graphical interface to simulate DFTs interactively. This allows us to validate DFTs and understand the behavior of dynamic gates.
• Exact & 100% bounded results: Its analysis results are exact or bounded with a 100% guarantee (thanks to probabilistic model-checking and BDDs) in contrast to statistical results via e.g., Monte-Carlo simulation. Moreover, the precision of results can be adjusted up to 16 decimal places.
• Rich set of importance measures: It verifies a range of importance measures like Birnbaum Index, Criticality Index, RAW, RRW, Diagnostics Importance Factor, Fussell-Vesely, BAGT+, BAGT-, etc., on DFTs.
• Embedding Markov chains: It allows defining failure probabilities of basic events in fault trees using Markov chains.
• Wide range of measures: It allows for verifying a range of measures specified in continuous stochastic logic (CSL) instead of only two measures, Reliability and MTTF. It categorizes metrics based on their complexity: Basic, Advanced, Importance, and Custom.
  Basic

  • Reliability: the probability of failure within a given time bound.
  • Unreliability: the complement of reliability (1- Reliability).
  • Average failure probability per hour
  • Mean-time-to-failure: the expected time to system failure or scenario occurrence.
  • Event probability within a time bound: the probability that an event occurs within a given time.
  • Event probability: the probability that an event occurs.
  • Instantaneous probability: the probability that an event occurs at a given time.
  Advanced

  • Full function availability (FFA): the time-bounded probability that the system provides full functionality, indicating it has neither failed nor degraded.
  • Failure without degradation (FWD): the time-bounded probability that the system fails without being degraded first.
  • Mean time from degradation to failure (MTDF): The expected time from the moment of degradation to system failure.
  • Minimal degraded reliability (MDR): the worst-case failure probability when using the system in a degraded state.
  • Failure under limited operation in degradation (FLOD_1): the probability of failure when imposing a time limit for using a degraded system.
  • Failure under limited operation in degradation (FLOD_2): similar to FLOD_1, but with additional conditions of avoiding prior system failure.
  • System integrity under limited fail-operation (SILFO): it considers the system-wide impact of limiting the degraded operation time, with aspects FWD and FLOD_1.
  • Reach-avoid probability: the probability of one event occurring without another event happening before.
  • Time-bounded reach-avoid probability: the probability of an event occurring within a time limit without another event happening beforehand.

  
  Importance

  • Birnbaum index (BI): it measures how much the system's unreliability depends on a specific component's unreliability.
  • Criticality importance (CI): similar to BI, scaled by the ratio of component and system unreliability.
  • Risk achievement worth (RAW): the impact of a component's total degradation on system unreliability.
  • Risk reduction worth (RRW): the impact of making a component fully reliable on system unreliability.
  • Diagnostics importance factor (DIF): the frequency of a component's failure in states where the system has failed.
  • BAGT+: the change in mean time-to-failure (MTTF) if the component fully degrades.
  • BAGT-: the change in mean time-to-failure (MTTF) if the component is fully reliable.

  
  Custom

  Custom properties can be specified using Probabilistic Computation Tree Logic (PCTL) / Continuous Stochastic Logic (CSL).

  The probability measure on Markov models is typically defined on paths. These paths are defined as in temporal logic, or more specifically computation tree logic (CTL), a branching-time logic. That means that the formula alternates over descriptions of paths and descriptions of states.

  Path Formulae

  For this, we assume that a and b are state formulae and {op} is any one of <, <=, =, >=, >. The available path formulae are:

  • a U b to describe paths on which at some point b holds and in all prior steps a holds.
  • F b as a shortcut for true U b.
  • a U{op}k b (where k is an expression evaluating to a number) to describe the paths on which b holds within k time (where time in discrete models means steps) and a holds before.
  • F{op}k b as a shortcut for true U{op}k b.
  • G a to describe paths on which a holds in every step.

  State Formulae

  Here, we assume that a and b are state formulae, phi is a path formula and {op} is any one of <, <=, =, >=, >. The available state formulae are:

  • c where c is either a label or an expression over the model variables.
  • a | b, a & b to describe all states that satisfy a or b, a and b, respectively.
  • !a to describe the states not satisfying a.
  • P[{op}]t [ phi ] (where t is a threshold value) to describe the states in which the probability to satisfy phi conforms to the comparison {op} t.
  • LRA[{op}]t [ a ] to describe states in which the long-run average probability to be in a state satisfying a conforms to {op} t.

  Obtaining Probabilities

  Although formally not allowed in PCTL/CSL, one can also request the probability of fulfilling a path formula from each state. Instead of comparing to a given value P{op}b [ phi ] , one can write P=? [ phi ] to obtain the actual values rather then obtaining a truth value.

  Nondeterministic Models

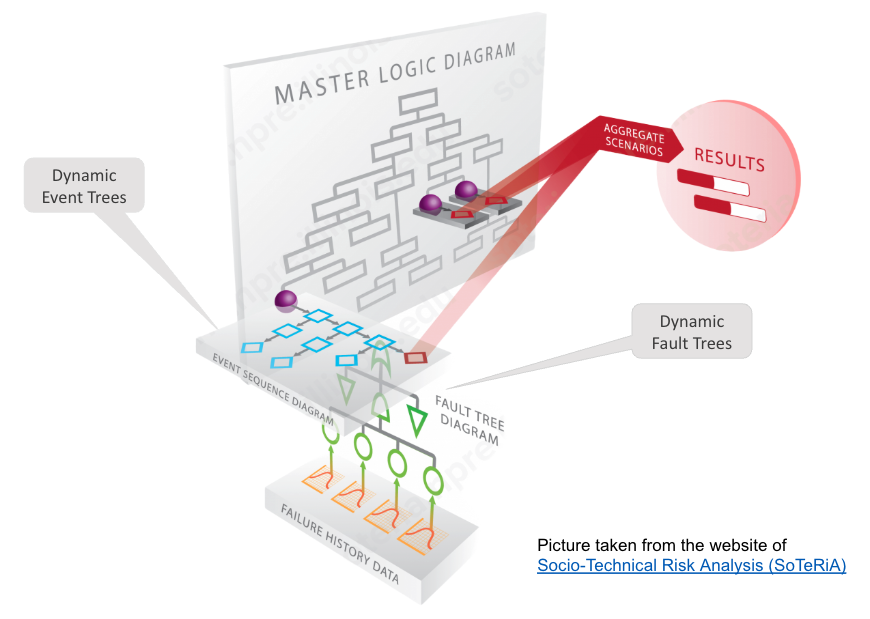
  For nondeterministic models, the formula can (and sometimes needs to) specify whether it refers to minimal or maximal probabilities. Since there is no information on how the nondeterminism in the models is to be resolved, Storm needs information on whether it should resolve the choices to minimize or maximize the values. That is, you cannot write P=? [F a], but have to either write Pmin=? [F a] or Pmax=? [F a]. While you can also specify min and max when comparing to a probability threshold, it's not necessary to do it. By default, if the comparison operator {op} is < or <=, then the probability is maximized and otherwise minimized. The reasoning is the following: if the property holds in a state, then no matter which resolution of nondeterminism is taken, the probability will always be below (or equal) to the threshold value.

• Embedding DFTs: It allows for the embedding of DFTs in event trees.
• Quantification of figures: It allows for quantifying figures like monetary loss, radioactive emission, etc., in event trees that may result as a consequence of accidental events.
• Sequence of decisions: It allows for modeling and analyzing a sequence of decisions, each having probabilistic outcomes, by system operators, allowing for worst- and best-case analysis in event trees.
• Living PRA: It allows for analyzing dynamic event trees/risk models in an interactive fashion. At each node of the model, users can figure out which decision will maximize/minimize the probability of consequences under the current environmental conditions (e.g., temperature, pressure, etc.). Note that the environmental conditions may not remain static throughout the analysis; rather, they may change as we move from one node to another in the model.
• Analysis: By analyzing event trees, we get:
  • Expected gains or losses, such as radioactive leakage, fatalities, etc.,
  • Max/min limits on the frequencies of the consequences, and
  • Wise choices to, for example, lessen the unfavorable effects/outcomes.

SAFEST enables the graphic construction of master logic diagrams (MLDs). MLD is a logical decomposition of the general undesirable end state that is displayed at the top of the tree and progresses to more precise event descriptions at lower levels. The leaves of the tree represent the fundamental initiating events (IEs).

• IEs are attached to event trees that model all possible consequences of IEs along with the control functions and the decisions of operators to mitigate the impact of bad consequences.
• The control functions in event trees are attached to dynamic event trees (DFTs) modeling their failure behavior. Quantities like radioactive emissions, casualties, monetary loss, etc, can also be specified in event trees.
• Analysis: The analysis of MLD computes the maximum and minimum probabilities (expected values) of consequences (quantities), allowing for the analysis of best and worst-case scenarios.
• Autmatic generation of models: SAFEST enables automatic generation of master logic diagrams from FMECA tables.

• Scalability: It is highly optimized for scalability and can analyze very large Markov chains — even those with billions of states — depending on the model type, encoding, and available hardware.
• Graphical Modeling: It enables graphical modeling of Markov chains – even those with billions of states – in a compact way. One can assign labels to any state using Boolean logic equations on state variables.
• System Rewards: It enables attaching rewards to states and transitions of Markov chains, and can compute their expected values.
• Compositional Modeling: It supports compositional modeling of systems, i.e., sub-systems of a system are modeled independently, which can then synchronize on common actions to generate a monolithic model of the overall system.
• Interactive Simulation: It provides a graphical interface to interactively simulate Markov models. One can decide which sub-system will change its state (perform a transition) in the next time-step. If a transition is synchronous, then every participating sub-system will change its state. It is extremely useful for debugging extremely large Markov chains.
• Wide Range of Measures in CSL logic: It supports continuous stochastic logic to write properties to be verified on Markov chains. Most commonly used properties are predefined in the tool. A few examples are:
  • Steady-state analysis
  • Expected visiting time analysis
  • Reachability properties
  • Step/time-bounded reach-avoid probabilities
  • Expected cumulative rewards
  • Steady-state probability
  • Instantaneous probabilities
  • etc.
• Formally Verified Algos: All analysis algorithms in SAFEST are formally verified and published internationally.

Bowtie analysis is the most used risk assessment method. It is unique in its ability to visualize complex risks in a way that is understandable, yet also allows for detailed risk-based improvement plans. A bowtie diagram presents the danger you face in a single, understandable picture. It is simple to discern between the proactive and reactive facets of risk management thanks to the diagram's bowtie-like shape. It summarises several possible event scenarios and shows the measures you have in place to handle them. Designed with the end user in mind, the software is among the most user-friendly risk assessment tools. Using it to create a diagram is easy, and the application lets you update the diagram to reflect the current condition of your safety barriers.

• Protocals visualization: The bowtie technique clearly shows your risk management plan and arranges the major hazards facing your organization. The barriers in the bowtie diagram show the controls you have in place to prevent, reduce, or eliminate serious outcomes. Holding barriers accountable makes it obvious what everyone needs to do to operate safely. By giving precise daily operating information, operational staff can take ownership of the bowties when they are involved in their construction. You can use models to see your safety protocols on the diagram. Every action can be connected to the barrier it supports. Finding safety-critical actions that are performed to guarantee the ongoing integrity of risk barriers is the primary goal of the SMS. When all the data is shown on the bowtie, everyone can see the full risk context and the tasks they are responsible for.
• Assessment & accountability: Once a bowtie diagram has been created, you can assess and look over the safety measures you've implemented. Among other things, these barriers can be classified according to their type, effectiveness, and accountability. Examine the efficacy of your barriers to obtain instant visual insight into their strength. By examining the various types of obstacles, you can increase the organization's resilience and reduce the chance of common mode failure. Color coding is commonly used to show how effective hazardhive barriers are, which can be customized to your needs. Customizable job titles can be used to connect accountability to barriers. This makes it easier to understand who is in charge of maintaining safety barriers. It increases ownership of barrier performance and makes clear what everyone must do to operate safely.

• Parameter estimation: It allows for estimation of (parameters of) failure distributions from the failure data of components.
• Mixture distribution: It enables combining failure distributions by assigning weights to them, which helps combining, for example, failure distributions from international reliability standards with empirical distributions (calculated from field data) allowing for having more meaningful insights of systems.